先週木曜(2014/8/7)のPFIセミナーで表記のタイトルで発表したので，その資料を公開します．
7月にコペンハーゲンで開かれた理論計算機科学の学会に行ってきたときの話を雑多に書いています．
僕が会議に参加した時の発表スライドも公開しています．
本日のPFIセミナーは泣く子も黙るレッドコーダー、最近はKDDベストペーパーランナーアップ受賞でも旋風を巻き起こした新入社員：楠本（@ir5）がICALP 2014 参加記 についてしゃべります。ご期待ください！！！
— PFI official account (@preferred_jp) August 7, 2014なんですかこの煽りは… (困惑)
— *IRUN (@ir5) August 7, 2014M.Kusumoto, and Y.Yoshida . "Testing Forest-Isomorphism in the Adjacency List Model." ICALP 2014, to appear.
修論の成果で投稿した論文が国際会議のICALP2014に採択されました．
ICALP(International Colloquium on Automata, Languages and Programming) は理論計算機科学(理論系アルゴリズム，計算量理論，言語・オートマトン，プログラミング言語理論など) を扱う国際会議です．運営はEATCSというヨーロッパの理論計算機科学の団体によって行われ，会議は毎年ヨーロッパの色々なところを転々としながら開催されるようです．今年はデンマークのコペンハーゲンで開催されます．
ICALPは理論系アルゴリズム界隈の会議の中でも上位レベルのものとして知られています．たとえば Microsoft Academic Search の引用数順で会議一覧を見てみると，上から4番目にあることが分かります．(共著者の吉田さん曰くヨーロッパ内の会議ではトップとのこと．)
論文は NII の吉田さんとの共著です．吉田さんは後述する性質検査アルゴリズム分野のプロで，今回の論文もその性質検査アルゴリズムに関するものになっています．
論文はざっくり言うと「木の同型性判定を，入力グラフのごく一部分だけを見て近似的に解くためのアルゴリズムの提案」がメインです．
グラフ同型性判定問題とは，2つのグラフが与えられたときに，頂点の名前を付け替えることで2つを全く同じものにすることが可能かどうかをyes/noで答える問題です．
例えば下の図のようなグラフが入力なら A→1，B→2，… という付け替えをすることで同じものにできるのでyes(同型)であると答えるのが正解，といった感じです．
さて，冒頭で「入力のごく一部分だけを見て解く」と書いたのですが，普通に考えるとそんなことは不可能です．例えば，辺が全く無いグラフと，辺が1本だけあるグラフが同型かどうか調べたい場合，同型ではない証拠としてその1本だけある辺を探さなければならないので必然的にグラフ全体を見ることになってしまいます．
しかしここで問題をある程度緩和し，アルゴリズムが乱択になるのを許すことで，入力を一部だけ見て同型性判定問題を解けるようになります．
$n$ をグラフの頂点数とし，また，問題の緩和のためにパラメータ $0<\varepsilon<1$ を導入します．論文では，オリジナルのyes/no判定問題を，「2つの入力グラフが同型である」か「一方のグラフの辺を $\varepsilon n$ 本追加・削除したとしてももう一方のグラフに同型に出来ない(つまり同型から程遠い)」かの2つを区別する問題に緩和します．そのうえで，この問題がグラフの $\mathrm{polylog}(n)$ 箇所だけを見ることで任意に高い確率で解くアルゴリズムを構成しました．$\mathrm{polylog}(n)$ は $n$ が十分大きいとき，$n$ に比べてずっと小さいということに注意してください．
このような風にして問題を緩和して解く分野が性質検査と呼ばれる分野です．性質検査では，緩和した問題を解くことを「検査する」と呼んだりします．
性質検査分野は1998年前後あたりから O.Goldreich や D.Ron らによって理論界隈で提唱された比較的新しい分野です．問題を緩和しているとはいえ線形時間より真に高速に解ける(爆速)，理論的にも大掛かりな道具や手法が満載ということで，理論系アルゴリズムのトップ会議(STOC,FOCS,SODA)でも毎年何本か論文が採択されています．
理論屋の主な興味は，問題を緩和することによって，どのような特徴を持った問題が解けるようになるのかをある程度包括的に調べることです．つまり，さきほどの節で問題を緩和して解けるようにするみたいなことを書きましたが，緩和しさえすればどんな問題でも解けるようになるというわけではなく，依然として(入力を全部見ないと)解けないものもいっぱいあるので，それを理論的にまとまった形で分類したい，ということです．
性質検査の枠組みの中で知見が深められている分野の1つがグラフ理論です．入力が密グラフ(隣接行列)である場合は「定数時間*1で検査できる性質の必要十分条件」が知られており，疎グラフ(隣接リスト)の場合も，各頂点の次数がある定数以下であると入力に制限が付いている場合はある程度広い性質が定数時間で検査できることが知られています．
ところが疎グラフで次数の制限が無い場合がどうなのかということについては，あまりよく知られていませんでした．もともと次数制限版ばかり考えられていたのはその方が問題が解きやすくなるからという面があるのですが，次数制限されたグラフというのはグラフ全体からするとかなり限られたものになってしまっています．
問題が解きやすくなるというのは，たとえば，次数が制限されていれば頂点をランダムに選んでそこから距離が定数の部分を全部探索するといったことができますが，次数の制限が無い場合はそういったことはできません．なぜなら，探索している最中で次数がとても大きい点に突っ込んでいってしまった場合，そこにつながっている辺を全て見ると多くの部分を見る羽目になってしまうからです．
そこで，解ける範囲で入力をある程度制限しつつも，次数の制限を外した場合にどういった性質が検査できるのか? という課題に我々は焦点を当てました．入力が木であるのはだいぶ制約として強い気がしますが，それでも証明するのは全く自明ではありません．
また，論文では同型性判定を道具にして，入力として木が与えられたとき，任意の性質を $\mathrm{polylog}(n)$ 箇所だけ見ることで検査できることを証明しました．この証明には STOC'11 の Newman, Sohler が使った手法と類似のものを用いています．
ここからは回想です．今回の結果はなかなか難産でした．まず修士1回生あたりのころからどういう問題に取り組めばよいかどうかをずっと模索していた気がするのですが，最初に目星を付けた問題が実はよく調べてみると既に解かれていたり，そもそも取り組むべき問題を探したところでそれが解けるのかどうかよく分からなかったりと色々遠回りをしました．今回の問題に取り組むことが決まったのは修士1回生の終わりの頃でした．
証明の方針自体は最初からなんとなく決まっていたのであとはそれを細かく解析するだけだろうと思っていたのですが，いざ始めてみると細かい部分がとても大変で，一度は投げ出し気味になってしまいました．これが修士2回生の4月～6月頃です．で，さすがに放置するのもなんなので一旦まとめて別のある会議に出したものの，しばらくしてから見返してみると証明がかなりいい加減で，会議からnotificationが返ってきたあたりから本格的に修正していきました．このとき会議から返ってきた査読のレビューがかなり的確で，ある意味無くしていたモチベーションを回復するきっかけになったような気がします．これが修士2回生の12月～1月あたりです．1月は本当に証明の修正や，論文の流れを追いやすくするために証明の概要を章の冒頭に書いたりをひたすらやっていました．
アルゴリズムの厳密な計算量は $\log(n)^{2^{\mathrm{poly}(1/\varepsilon)}}$ とかになっていて実用的には超マッシブなのでそのまま実用で使うのは難しいと思われる，理論と実用のギャップはとても大きい．
*1:問題の緩和の際に導入したパラメータ$\varepsilon$は定数だと見なします
2014年になってからだいぶ経ちましたが2013年の進捗を振り返ろうかと思います．
プログラミングコンテスト絡みのことはTopCoder部の方に書いたのでそっちを御覧ください．
Kusumoto Mitsuru, Yuichi Yoshida, and Hiro Ito. Constant-Time Approximation Algorithms for the Optimum Branching Problem on Sparse Graphs. (IJNC'13)
卒論の成果をIJNCというジャーナルに投稿して，何度かの修正を経て収録されました．ここに投稿する前に ICNC (dblp) という会議で発表したのですが，これはそのジャーナル版にあたります．
内容としては，最大重み有向森問題という有向グラフの最適化問題があるのですが，その問題の最適値の値を，グラフのごく一部分だけを見て近似的に計算するアルゴリズムを提案した，というものです．最大重み有向森は最小有向木問題と等価(互いに多項式時間帰着可能)な問題として知られていて，組合せ最適化とかにも載っています．
この論文はここに落ち着くまでにいくつか別の国際会議に出して落ちるといったことを繰り返していて，割と色々な場所を彷徨っていました．中には結構惜しいところ(というか半ば理不尽っぽい感じのレビュー)でRejectを受けたりしたものもあって悔しい思いをしたというのが正直なところです．今回収録されてとりあえず成仏された感じになりました．
研究関係のこと(理論計算機科学とか離散数学)でもっと体系的な知識を付けたいと思ったので，4月から新B4生達も交えてラボ内で輪講をしました．とりあえず読んだのは N.Alon と H.Spencer の Probabilistic Method と，D.Spielman の Spectral Graph Theory の2つです．
Probabilistic Method は確率事象を考えることによって存在性を示したり何かの上界や下界を証明する手法のことです．ラムゼー理論のような，普通にやったらどうやって解析すればいいのかよくわからない感じの問題が多く扱われています．できるだけ読み飛ばさないスタイルで，しかも結構ゆっくりと進めたので，1年で読むことができたのは本の30%くらいでした．それでも解析のための様々なテクニックを丁寧に見ることができたのは良かったかもしれません．(実際の場面で活用できるかというとそれはまた別の話かもしれませんが．)
Spectral Graph Theory はグラフを隣接行列やラプラシアンの固有値の観点から解析する手法で，いろいろなところに応用があります．ここでやったことは9月のPFIセミナーの発表資料にひと通りまとめています．普通にスペクトルグラフについて詳しくなれたほかに以前と比べて線形代数に強くなった(気がする)ので学べたことは多いと思います．ひとまず興味のあるところは読み終えたので，せっかくなので次はスペクトルグラフのテクニックを使った論文を読んでみよう，みたいになっています．
Danushka Bollegala, Mitsuru Kusumoto, Yuichi Yoshida, and Ken-ichi Kawarabayashi, Mining for Analogous Tuples from an Entity-Relation Graph. (IJCAI'13)
僕は2012年の後期から河原林巨大グラフプロジェクトでRAをやっているのですが，そこで東大のダヌシカ先生たちと共同で研究をして投稿したところ，IJCAI(AI系のトップ会議)に採択されたので発表に行ってきました．
僕自身は主にアルゴリズムの実装と実験を担当して second author という位置づけだったのですが，first author のダヌシカ先生が別件で会議に出られないとのことだったので僕が行って発表することになりました．
開催場所は北京でした．噂に聞いていたとおり空気が悪かったので呼吸に気をつけながら滞在しました．
AIは専門外の分野だったので発表を聞いてもわからないことも多かった(というかそもそもAI自体が様々な分野の集合体なので…)のですがどういう問題が重要とされているかとかどういう手法がメジャーなのかとかはなんとなく分かった気がします．
修論で成果が出ていたり，他にも何かしているような気がするのでそれらを何らかの形にして publish したいです．
これは Competitive Programming Advent Calendar Div2013 の 20 日目の記事です．最近点対問題の話をします．
最近点対問題は，空間上に点の集合が与えられた時に，その中で最も距離が近いペアを探す問題です．
応用としては，何らかのオブジェクトを特徴ベクトルに写した後で，最も類似したペアを探したいときなどに役に立つのではないかと思います．競技プログラミング界では，今年のICPC会津大会で3次元上の最近点対問題が出題されました．
空間が平面のときは分割統治による $O(n\log{n})$ 時間アルゴリズムが有名かと思います．今回は一般の次元で，(ハッシュマップを用いて)線形時間で動く実装が楽そうな乱択アルゴリズムの紹介をします．参考にした文献は以下のサーベイです．
Smid, Michiel. Closest point problems in computational geometry. MPI Informatik, Bibliothek & Dokumentation, 1995.
11/2にFOCS2013読み会に参加してきたのでその要約を書いてみます．FOCSは理論計算機科学のトップ会議の1つです．
※なんか理解が浅かったり間違えたまま把握してたりしてテキトーなことを書いてしまっているかもしれませんがご了承ください．
離散変数に関する中心極限定理の話．
$\{0,1,\cdots,k\}$ を取る確率変数 $X_1, \cdots, X_n$ と，$S = X_1 + \cdots + X_n$ があるとする．各 $X_i$ は互いに独立であるが，それぞれ異なる分布に従うかもしれないとする．確率変数 $S$ の値を何回か確率分布に沿ってサンプリングして， $S$ の分布を $\varepsilon$-近似したい．(正確には，見積もった分布と本当の分布の分散が $\varepsilon$ 以下になるようにしたい．) 何回くらいサンプリングが必要か? ここで，$k$ は定数で，$n$ は十分に大きい数であるとみなします．
この論文では $O(poly(k, 1/\varepsilon))$ 回のサンプリングで近似できると主張しています．元の値が $0$ から $kn$ と広い値を取るのに対してサンプル回数は $n$ に依存しない回数で済むということを考えると，これは強力な結果であるように見えます．
各 $X_i$ がすべて同じ分布に従うなら中心極限定理で終わり？ですが，そうでないので難しい(はず)．$k=2$ のとき (つまり各変数が0か1しかとらない場合) には2012年に既存研究があって，中心極限定理により正規分布で近似できる(らしいです)．ところが，$k=3$ のときは単なる正規分布ではだめで，たとえば $n=50$ で，$X_1, ..., X_{49}$ は $\{0, 2\}$ を等確率で取り，$X_{50}$ は $\{0, 1\}$ を偏った確率で取るような場合，$S$ の値が偶数を取るときと奇数を取るときで振る舞いが変わってしまう．
このような複雑な振る舞いを解析したのが本論文の結果で，以下の構造定理にまとめられます．
構造定理. ある $c \in \{0, 1, \cdots, k-1 \}$ が存在し，$S$ は "$c \cdot$ (離散の正規分布) $+\{0,1,\cdots,c-1\}$ の任意分布のランダム変数" で近似できる．
つまり，離散変数の和にはなんらかの周期性が必ず出て，周期ごとに分解するとそれぞれは正規分布に従っているとみなせる，というものです．アルゴリズムはこの定理をほとんどそのまま使って導出できる模様です．
証明は，まず周期性が無い場合について考え，次に周期性がある場合について考えるために各 $X_i$ の値域を小さいステップに対応する部分と大きいステップに対応する部分の2つに分割して解析するっぽいです．(このへんはよくわかりませんでした)
今後の発展として，$k$ がconstantでない場合どうなのかとか，$k=2$ の場合は機械学習に応用があるらしいけど $k \ge 3$ の場合どうなのかということが挙げられていました．
(概要だけ)
リプシッツ連続で強凸というクラスに属する関数 $f$ が与えられるので，それを最小化する問題(つまり $\min_x f(x)$ を計算する問題)に関する新しい反復型のアルゴリズムを提案．
この問題では今までに「座標勾配法」と「加速勾配法」というものが知られていた．
それぞれ，
というメリットがあり，今回はそれらを組み合わせた手法を考案した．
アルゴリズムの性能の評価には，Estimate sequence という1983年くらいの結果を確率変数に拡張したものを使うらしいです．
著者の Marek Cygan はFPT関係の分野で様々な成果を出しています．またプログラミングコンテストでも強い人として有名なので知ってる人は知っているかもしれません．
この論文では，$k$-set packing という問題に対して既存のものより良い精度の近似アルゴリズムを与えます．
集合族 $\mathcal{F} \subseteq 2^U$ が与えられる．$\mathcal{F}$ の内の各集合の大きさはちょうど $k$ である．
$\mathcal{F}$ からできるだけ多くの disjoint な集合を選びたい．最大でいくつ選べるか?
set packingは有名なNP完全問題であり，近似もそれなりに難しい問題として知られています．$O(|U|^{1-\varepsilon})$ 近似困難?) 既存研究で知られていたのは以下のとおりです．
今回はこの交換という操作を拡張したものを考えます．
交換というのは次のようなものです：
confliction graph を，$\mathcal{F}$ 内の各集合を頂点とし，もし2つの集合が disjoint でないなら枝を張ってできるグラフとします．($\mathcal{F}$で独立な部分集合族はこのグラフ上の独立頂点集合に対応することに注意)
いま，$\mathcal{F}$ の中からいくつかの集合を選んでいる状況を想定します．$X$ を今選んでる頂点集合とします．
improving set を，conflict graph 内の独立頂点集合 $Y$ で，$|X \cap N(Y)| < |Y|$ となるものとします．このとき，いま選んでる集合の中から $Y$ と隣接するものを捨て，代わりに $Y$ を足すと解が改善されることに注意します．
できるだけ大きい improving set が見つけることができれば解を改善できて嬉しいです．交換する集合のサイズ $|Y|$ が大きいほどなんとなく良いような気がする(?) んですが，問題はこの交換という操作は普通にやると計算時間が多項式にならないということにあります．
そこで，この論文ではpathwidthというグラフの指標を使い，うまく近似解を得ます．
重みのついた無向グラフが与えられる．点連結度が $k$ になるような部分グラフで，コスト最小のものを取りたい．
制約が枝連結度なら近似度2で解けるらしいが，点連結度だと難しいらしい．既存研究では以下のことが知られていた．
今回は，$n \ge k^3$ ならば6近似可能ということを示したようです．(近似度の改善)
手法はiterative rounding という手法を用いる模様．
頂点重みのシュタイナー木を考えます．シュタイナー木 $T$ のコストを $w(V(T)) + p(V \setminus V(T))$ で評価するとします．(シュタイナー木に入っていない頂点にもコストがかかる) この問題は集合被覆を含んでいるので近似アルゴリズムを考えることになります．普通，この問題に対する $\alpha$-近似解 といったら，次のようなものです．
$w(V(T)) + p(V \setminus V(T)) \le \alpha w(V(T^*)) + \alpha p(V \setminus V(T^*))$
この論文では LMP (Lagrangean-multiplier-preserving) というものを扱います．次のようなものです．
$w(V(T)) + \alpha p(V \setminus V(T)) \le \alpha w(V(T^*)) + \alpha p(V \setminus V(T^*))$
(左辺の第二項に $\alpha$ がかかっていることに注意．)
これだけ見ると何やってるんだかよく分かりませんが，LMPが解けると quota problem, budget problem 等，他の問題が$\alpha$-近似で解けるようになって嬉しいようです．
で，既存研究で，既に LMP で $O(\log{n})$-近似するアルゴリズム (STOC'01) があったのですが，今回はなんとその結果にミスがあったことを指摘し，新しいアルゴリズムを提案しました．テクニック的にはかなり高度なことをしているっぽいです．
オンラインで頂点重みシュタイナー森を計算する問題です．またしても頂点重みシュタイナーなんちゃらで，しかも今度はオンラインというタフな設定です．(発表者の福永さん曰く今は頂点重みがキテいる!! とのこと．)
競合比 $O(\log n)$ で解けるらしいです．
ビンパッキング問題という有名な問題に対する近似アルゴリズムの提案．
問題設定はとてもシンプルです：$n$ 個のアイテムがあり，それぞれの大きさは $x_1,\cdots,x_n$ $(0\le x_i \le 1)$ である．大きさがちょうど 1 のビンを何個か用意して全てのアイテムをビンに詰めるとき，何個ビンが必要になるか計算せよ．
この問題はNP困難問題であり，近似アルゴリズムの研究がされてきました．最も新しかった結果は1982年の $APPROX \le OPT + O(\log^2 OPT)$ で，それ以降更新がありませんでした．
で，今回の論文は，これを更新し， $APPROX \le OPT + O(\log OPT \log\log OPT)$ にした，というものです．(全然更新できてないやんって感じだけど，有名な問題で30年以来改善されていなかったものを改善したのでこれはすごいことなのである．)
手法はLPのrounding的なテクニックを使うらしいですが，道中で Discrepancy theory でできたツールを使うようです．
この会が終わった直後くらいにこの記事書いて公開しようと思ってたのだけど色々やることがあって放置していたら1ヶ月半も経ってしまっていた．
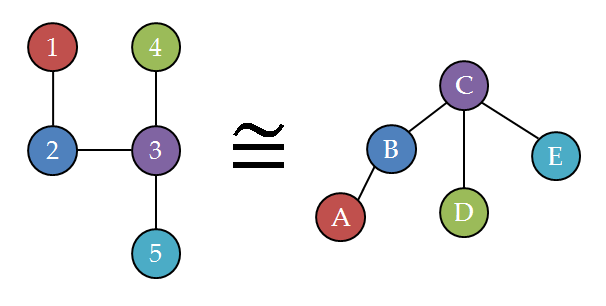
エントリのタイトルの定理について．天下一プログラマーコンテスト2013に出題された問題で知ったのでメモする．
ざっくり言うと「平面グラフ上でソース頂点集合とシンク頂点集合が指定された時，vertex-disjoint なパス集合の個数を行列式で計算できるようにする」定理です．なんでも組み合わせ界隈では結構有名らしい．
↓こういうのに対して
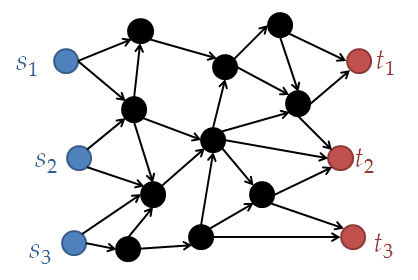
↓こういうのの個数を求める．
まずは準備から．言ってることは直感的なんだけどちょっと長い．
有向無閉路グラフ $G=(V,E)$ を考える．また，相異なる $2k$ 個の頂点 $s_1, s_2, ..., s_k, t_1, t_2, ..., t_k \in V$ を指定する．頂点 $s_1, ..., s_k$ のことをソース，$t_1, ..., t_k$ のことをシンクと呼ぶ．
また，$e(i, j)$ を頂点 $s_i$ から $t_j$ に向かう異なるパスの個数とする．
置換 $\sigma: \{1, ..., k\} \rightarrow \{1, ..., k\}$ に対して，$k$ 個のパスの組で $i$ 番目のパスが $s_i$ から $t_{\sigma(i)}$ に向かうものを $\sigma$-パスと呼ぶ．
さらに，$\sigma$-パスでどの2つのパスも vertex-disjoint ，つまり頂点を共有しないものの個数を $e(\sigma)$ で表すことにする．
さらに，$k \times k$ 行列 $M $ を $M_{ij} = e(i, j)$ とする．
任意の $\sigma \not= id$ に対して vertex-disjoint な $\sigma$-パスが存在しない，すなわち $e(\sigma) = 0$ ならば，$e(id) = \det(M)$である．
*1
DAG上でソースとシンクが指定されたとき，指定された各ソースとシンクの間の vertex-disjoint なパス組の個数を高速に計算できる．
各 $e(i, j)$ は定番 DP で簡単に計算できることに留意されたい．
普通の平面グラフに適応してもいいですし，例えば左と下方向にしか移動できないグリッドグラフなんかを考えると楽しそうな気配がしないでもないです．↓Wikipediaから画像引用
より一般に次のことを示します：$\det(M) = \sum_{\sigma} sign(\sigma) e(\sigma)$．
ここで，$sign(\cdot)$ は置換の符号．
まず行列式の定義から，$\det(M) = \sum_{\sigma} sign(\sigma) \Pi_{i=1}^{k} e(i, \sigma(i))$ です．積 $\Pi_{i=1}^{k} e(i, \sigma(i))$ は vertex-disjoint とは限らない $\sigma$-パスの個数です．
ソースからシンクに1対1に向かうパス組 $(P_1, ..., P_k)$ に対して $sign(P_1, ..., P_k)$ を (このパス組によって $s_1$ が向かう先のシンクの番号, $s_2$ が向かう先の番号, ... ) という置換の符号とすると，上記の式を少し変えて $\det(M) = \sum_{P_1, ..., P_k} sign(P_1, ..., P_k)$ と書けます．ここで添字の $P_1, ..., P_k$ はソースからシンクに行く全てのパス組を表すとします．さらに，
$\det(M) = \sum_{E' \subseteq E} \sum_{P_1 \cup ...\cup P_k = E'} sign(P_1, ..., P_k)$
のように変形して問題ありません．ここで内側の総和を $E'$ によって評価します．
i. $P_1 \cup ...\cup P_k = E'$ になるようなパス組が無いとき，外側の総和への貢献は 0 なのでそんな $E'$ は無視していいです．
ii. $E'$ が vertex-disjoint なパスを表していない時，$E'$ は下の図みたいにどこかで頂点を共有する形になっているはず．
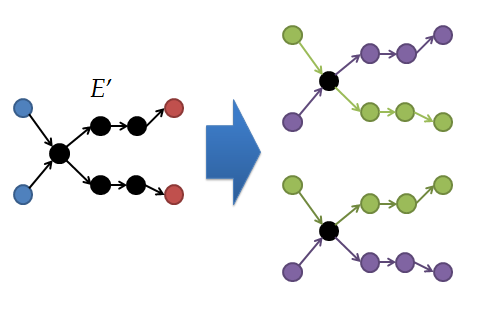
このとき，内側の総和にはこの共有する点でどう分岐させるかを入れ替えたパス組が存在することになるが，それらは互いに打ち消し合い，合計値は 0 になる．(置換の符号の性質．置換のどこか2項を入れ替えると符号が逆になる．)
よってこのとき外側の総和への貢献は 0 になるので，このときもそのような $E'$ を無視できます．
よって上記の式では $E'$ は vertex-disjoint なパスだけについて考えればよく，結果的に
$\det(M) = \sum_{\sigma} sign(\sigma) e(\sigma)$
が得られます．
本当は重み付きグラフでもいいらしいです．
*1:本当の定理はもっと一般的な形で表わされるんですがここでは簡単のためこのように記しています．
なんか最近アウトプットが全然無いなぁと思ったのでなんか書くことにします．
