エントリのタイトルの定理について.天下一プログラマーコンテスト2013に出題された問題で知ったのでメモする.
ざっくり言うと「平面グラフ上でソース頂点集合とシンク頂点集合が指定された時,vertex-disjoint なパス集合の個数を行列式で計算できるようにする」定理です.なんでも組み合わせ界隈では結構有名らしい.
↓こういうのに対して
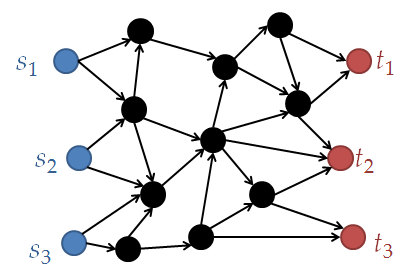
↓こういうのの個数を求める.

定理のステートメントの準備
まずは準備から.言ってることは直感的なんだけどちょっと長い.
有向無閉路グラフ $G=(V,E)$ を考える.また,相異なる $2k$ 個の頂点 $s_1, s_2, ..., s_k, t_1, t_2, ..., t_k \in V$ を指定する.頂点 $s_1, ..., s_k$ のことをソース,$t_1, ..., t_k$ のことをシンクと呼ぶ.
また,$e(i, j)$ を頂点 $s_i$ から $t_j$ に向かう異なるパスの個数とする.
置換 $\sigma: \{1, ..., k\} \rightarrow \{1, ..., k\}$ に対して,$k$ 個のパスの組で $i$ 番目のパスが $s_i$ から $t_{\sigma(i)}$ に向かうものを $\sigma$-パスと呼ぶ.
さらに,$\sigma$-パスでどの2つのパスも vertex-disjoint ,つまり頂点を共有しないものの個数を $e(\sigma)$ で表すことにする.
さらに,$k \times k$ 行列 $M $ を $M_{ij} = e(i, j)$ とする.
定理のステートメント
任意の $\sigma \not= id$ に対して vertex-disjoint な $\sigma$-パスが存在しない,すなわち $e(\sigma) = 0$ ならば,$e(id) = \det(M)$である.
*1
利点
DAG上でソースとシンクが指定されたとき,指定された各ソースとシンクの間の vertex-disjoint なパス組の個数を高速に計算できる.
各 $e(i, j)$ は定番 DP で簡単に計算できることに留意されたい.
普通の平面グラフに適応してもいいですし,例えば左と下方向にしか移動できないグリッドグラフなんかを考えると楽しそうな気配がしないでもないです.↓Wikipediaから画像引用

証明
より一般に次のことを示します:$\det(M) = \sum_{\sigma} sign(\sigma) e(\sigma)$.
ここで,$sign(\cdot)$ は置換の符号.
まず行列式の定義から,$\det(M) = \sum_{\sigma} sign(\sigma) \Pi_{i=1}^{k} e(i, \sigma(i))$ です.積 $\Pi_{i=1}^{k} e(i, \sigma(i))$ は vertex-disjoint とは限らない $\sigma$-パスの個数です.
ソースからシンクに1対1に向かうパス組 $(P_1, ..., P_k)$ に対して $sign(P_1, ..., P_k)$ を (このパス組によって $s_1$ が向かう先のシンクの番号, $s_2$ が向かう先の番号, ... ) という置換の符号とすると,上記の式を少し変えて $\det(M) = \sum_{P_1, ..., P_k} sign(P_1, ..., P_k)$ と書けます.ここで添字の $P_1, ..., P_k$ はソースからシンクに行く全てのパス組を表すとします.さらに,
$\det(M) = \sum_{E' \subseteq E} \sum_{P_1 \cup ...\cup P_k = E'} sign(P_1, ..., P_k)$
のように変形して問題ありません.ここで内側の総和を $E'$ によって評価します.
i. $P_1 \cup ...\cup P_k = E'$ になるようなパス組が無いとき,外側の総和への貢献は 0 なのでそんな $E'$ は無視していいです.
ii. $E'$ が vertex-disjoint なパスを表していない時,$E'$ は下の図みたいにどこかで頂点を共有する形になっているはず.
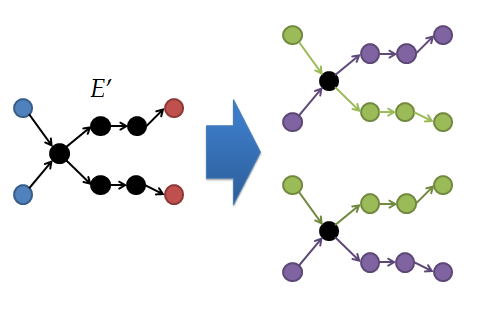
このとき,内側の総和にはこの共有する点でどう分岐させるかを入れ替えたパス組が存在することになるが,それらは互いに打ち消し合い,合計値は 0 になる.(置換の符号の性質.置換のどこか2項を入れ替えると符号が逆になる.)
よってこのとき外側の総和への貢献は 0 になるので,このときもそのような $E'$ を無視できます.
よって上記の式では $E'$ は vertex-disjoint なパスだけについて考えればよく,結果的に
$\det(M) = \sum_{\sigma} sign(\sigma) e(\sigma)$
が得られます.
ついでに
本当は重み付きグラフでもいいらしいです.
Referrence
*1:本当の定理はもっと一般的な形で表わされるんですがここでは簡単のためこのように記しています.