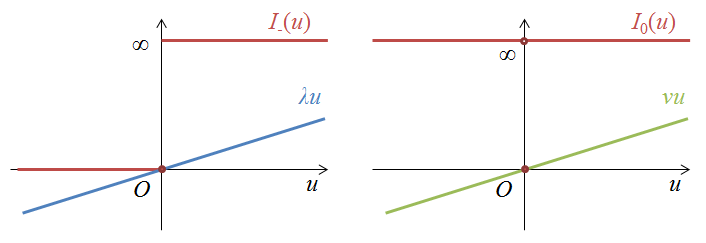ラグランジュ関数は以下のような形をした制約付き最適化問題を解くために導入される有名な手法です.
- $\min_{x \in D} f_0(x),$
- $\mbox{subject to}$
- $f_i(x) \le 0$ $(i=1,2,...,m)$
- $h_i(x) = 0$ $(i=1,2,...,p)$
- ここで,$D \subseteq \mathbb{R}^n$ は目的関数の定義域で, $f_0,f_1,\cdots,f_m, h_1, \cdots, h_p: D \rightarrow \mathbb{R}$ は任意の関数.
この記事では "Convex Optimization" (by Boyd and Vandenberghe) の5章 "Duality" の項を元に,ラグランジュ関数とその背後にある理論について記します.主に記したことは以下のとおりです.
- ラグランジュ関数の定義とその解釈の仕方について
- 強双対性が成り立つ関数のクラスについて
- その正当性の証明
キーワード:ラグランジュ関数,ラグランジュの未定乗数法,双対関数,KKT条件
この記事を書こうと思った理由
ラグランジュ関数は計算機科学の応用分野で重要になる手法であり,世の中には数多くのラグランジュ関数に関する説明があります.しかし,僕が目にした多くの説明は,直感的な説明に留めているものや,目的関数や制約関数について暗黙的に何らかの制約があるもの(例えばパラメータ表示可能である,といったような)についてのみ書かれている(それも恐らく厳密ではない)に過ぎないなど,不満に思っていた点がありました.このようにちゃんとした証明が添えられていない理由は詳細に立ち入ると難解になってしまうからでしょう.基礎分野ならともかく応用分野では飽くまでブラックボックスとして使えればよくて詳細に立ち入るのにあまり時間を割くのは本質ではないので,そうなってしまうのはしょうがないという面があるのだと思います.
しかし,ちゃんとした理由があまりわからないまま使うというのは怖いものです.実際には適応できないできない関数について手法を使ってしまって,とんでもない結果を導出してしまったりしうるからです.で,何か良い資料はないものかと先日会社の人に聞いたところ,上記の本 (Boyd本) に詳しく書かれていると教えてもらったので,それについて自分なりのまとめを記したいと思います.
Boyd本は pdf が無料で公開されているので誰でも読めますのでこの記事でよくわからなかったり詳しく知りたくなった方はBoyd本を見て下さい.ラグランジュ関数について書かれているのは5章からですが,大学1~2年生相当の数学の素養があれば途中からでも十分読めると思います.たまに前の章を少し読み返す必要があるかもしれませんが.
冒頭でも挙げましたが,以降では以下の最小化問題について考えていくことにします.特に明記しない限り,定義域,目的関数,各制約関数には制限を設けないことにします.この問題のことを主問題と呼ぶことにします.
- (再掲) $\min_{x \in D} f_0(x),$
- $\mbox{subject to}$
- $f_i(x) \le 0$ $(i=1,2,...,m)$
- $h_i(x) = 0$ $(i=1,2,...,p)$
主問題に対してラグランジュ関数 $L:\mathbb{R}^n \times \mathbb{R}^m \times \mathbb{R}^p \rightarrow \mathbb{R}$ は以下で定義されます.
\[
L(x, \lambda, \nu) = f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^p \nu_i h_i(x)
\]
$\lambda, \nu$ はそれぞれ $m $,$p$ 次元のベクトルです.$\lambda$ はラグランジュ乗数,また $(\lambda$,$\nu$) は双対変数と呼ばれます.
…で,突然なんなんだこの関数は,と思う人が多いんじゃないかと思うのですが,Boyd本ではこれについて良さそうな解釈が乗っていたのでそれについて記します.
"線形関数による置き換え" という見方
主問題は制約付き問題でしたが,以下のように書けば制約無しの問題に(強引に)書き換えることが出来ます.
\[
\min_{x \in D} f_0(x) + \sum_{i=1}^m I_{-}(f_i(x)) + \sum_{i=1}^p I_{0}(h_i(x))
\]
ここで,
- $I_{-} : \mathbb{R} \rightarrow \mathbb{R}$ は正のとき $\infty$,$0$ 以下のとき $0$ となる関数
- $I_{0} : \mathbb{R} \rightarrow \mathbb{R}$ は非0のとき $\infty$,$0$ のとき $0$ となる関数
です.要するに制約を満たさない場合に目的関数の値が $\infty$ になるように調整しているというだけです.
$I_{-}$,$I_{0}$ は $0$ 近傍でとても急激な変化をする関数です.ここで,新たにパラメータ $\lambda$,$\nu$ を導入し,急激に変化する関数 $I_{-}$,$I_{0}$ を線形関数で置き換えたものがラグランジュ関数という風に見なせます.(i.e., $I_{-}(f_i(x))$ → $\lambda_i f_i(x)$, $I_{0}(h_i(x))$ → $\nu_i h_i(x)$.)
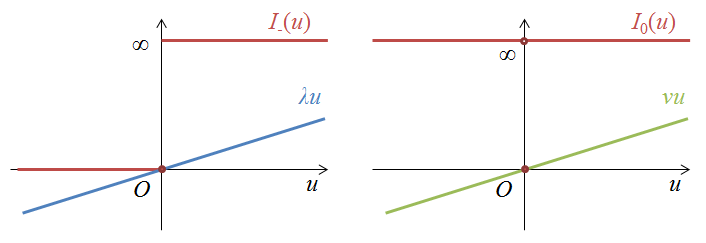
もちろんこの置換えはかなりいい加減で問題自体も大きく変わってしまっているのですが,適切なパラメータを選べばこの雑な置き換えでも主問題と同じような最適値を達成できるというのが後で述べるラグランジュ関数を考える利点です.
ラグランジュ双対関数 $g : \mathbb{R}^m \times \mathbb{R}^p \rightarrow \mathbb{R}$ は以下で定義されます.
先ほどの見方を踏まえているとこれは理解がしやすいです.パラメータ(というか双対変数) $\lambda$,$\nu$ で目的関数を"置き換え"た場合の問題の最適値です.
ラグランジュ双対関数は,(主問題の目的関数と制約関数がなんであれ)上に凸な関数になっています.これは, 型の不等式をラグランジュ関数に適応するとわかります:$\alpha \in [0,1]$ に対し,
型の不等式をラグランジュ関数に適応するとわかります:$\alpha \in [0,1]$ に対し,


ここで最後の式変形はラグランジュ関数が $\lambda$,$\mu$ について線形な関数であることを用いました.
弱双対性
ここで,$\lambda \ge 0$ だとする*1と,先ほどの図のように,$I_{-}(f_i(x)) \ge \lambda_i f_i(x)$, $I_{0}(h_i(x)) \ge \nu_i h_i(x)$ なので,任意の $x \in D$,$\lambda \ge 0$,$\nu \in \mathbb{R}^p$ に対して $g(\lambda, \nu) \le f_0(x)$ が成り立ちます.これを弱双対性と呼びます.
双対問題
$g(\lambda, \nu)$ は主問題の解の値を下からバウンドできます.ここで,このバウンドがどこまで成り立つのか,つまり $g(\lambda, \nu)$ はどこまで大きく出来るのかというのを考えるのは自然なことです.以下の問題を(主問題に対する)双対問題と呼びます.
- $\max_{(\lambda,\nu) \in \mathbb{R}^m \times \mathbb{R}^p} g(\lambda, \nu)$
- $\mbox{subject to}$ $\lambda \ge 0$
先ほど述べたように $g$ は上に凸であり,$\lambda$ の取りうる範囲も凸なので,双対問題は主問題に関係なく凸最適化問題になります.
$p^\star$ を主問題の最適解,$d^\star$ を双対問題の最適解とすると,弱双対性は $d^\star \le p^\star$ と表せます.
具体例
ここで1つ簡単な具体例を挙げます.最適化問題として以下の1変数の問題を考えましょう.
- $\min_{x_1 \in \mathbb{R}} (x_1-3)^2$
- $\mbox{subject to}$ $x_1^2 \le 1$
まぁこの程度の問題ならラグランジュ関数とか考える必要全く無いのですが細かいことは置いておきましょう.
この主問題に対するラグランジュ関数は $L(x_1, \lambda_1) = (x_1-3)^2 + \lambda_1 (x_1^2 - 1)$ です.また,ラグランジュ双対関数は  となります.
となります.
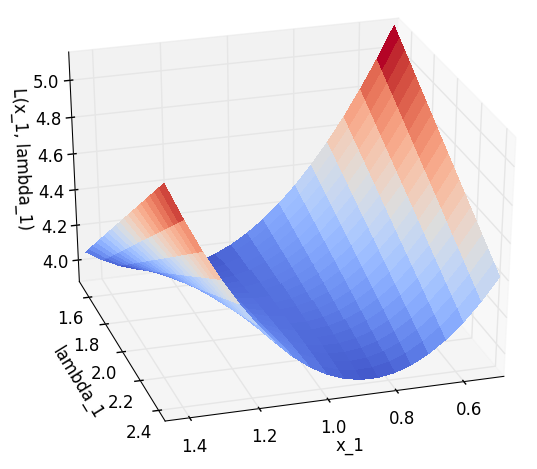
主問題の最適解は $x_1=1$ のときに $p^\star=4$,双対問題の最適解は $\lambda_1=2$ のときに $d^\star=4$ となります*2.
ラグランジュ関数は図示すると以下のようになります.(主問題,双対問題のそれぞれで最適解を取る点 $(x_1, \lambda_1)=(1,2)$ がなんとなく鞍点になってそうな雰囲気がします.)
強双対性
先ほどの具体例のように $d^\star=p^\star$ が成り立つとき,その問題について強双対性が成り立つと呼びます.強双対性が成り立てば,主問題の代わりに双対問題を考えれば良いことになり,双対問題の方が考えやすい場合には役立ちます.たとえば主問題では変数の個数は多いけど制約の個数が少ない場合,双対問題では変数の個数が少なくなるため,双対問題の方が考えやすいことが多いようです.
残念ながら強双対性は一般には成り立ちませんが,限られた条件下では成り立ちます.それを以下に記します.
凸な場合
以降は主問題が凸である場合を考えます.つまり,$f_0, f_1, \cdots, f_m $ が下に凸,定義域 $D$ が凸で,主問題が以下のような形式になっている場合です.
- $\min_{x \in D} f_0(x)$
- $\mbox{subject to}$
- $f_i(x) \le 0$
- $Ax=b$ ($A$ は $p \times n$ の行列)
以下では簡単のため等号制約の行列 $A$ は行フルランク($\mathbf{rank} A = p$) とします.
Slaterの条件 (凸な場合)
強双対性が成り立つための条件の1つとして,次のものをSlaterの条件と呼びます:ある $x \in \mathbf{int} D$ *3 があって,以下を満たす.
\[
f_i(x) < 0 (i=1,\cdots,m), Ax=b.
\]
つまりSlaterの条件とは,狭義に実行可能な点があるということです.
次の節では以下のことを示します.
補題.主問題が凸であり,Slaterの条件が成り立つとき,ラグランジュ関数について強双対性が成り立つ.
$\mathcal{G}$ を,$x$ を動かしたときに目的関数と制約関数が取りうる範囲とします:
\[
\mathcal{G} = \{f_1(x), \cdots, f_m(x), h_1(x), \cdots, h_p(x), f_0(x) \mid x \in D\}.
\]
このとき,ラグランジュ双対関数は

です.また,主問題の最適解は  と表せます.
と表せます.
また,$\mathcal{A}$ を,$\mathcal{G}$ の上側領域と右側領域とします.(エピグラフっぽいもの)
\[
\mathcal{A} = \{(u,v,t) \mid \exists x \in D, f_i(x) \le u_i, h_j(x) = v_j, f_0(x) \le t\}.
\]
$\mathcal{G}$ の定義は
\[
\mathcal{G} = \{(u,v,t) \mid \exists x \in D, f_i(x) = u_i, h_j(x) = v_j, f_0(x) = t\}.
\]
だったことを踏まえると $\mathcal{G} \subseteq \mathcal{A}$ に注意して下さい.
例えば先程の具体例の問題ですと, $\mathcal{G}$ は下図の青色曲線,$\mathcal{A}$ は赤色領域に対応します.ここで横軸が $u$,縦軸が $t$ に対応します.
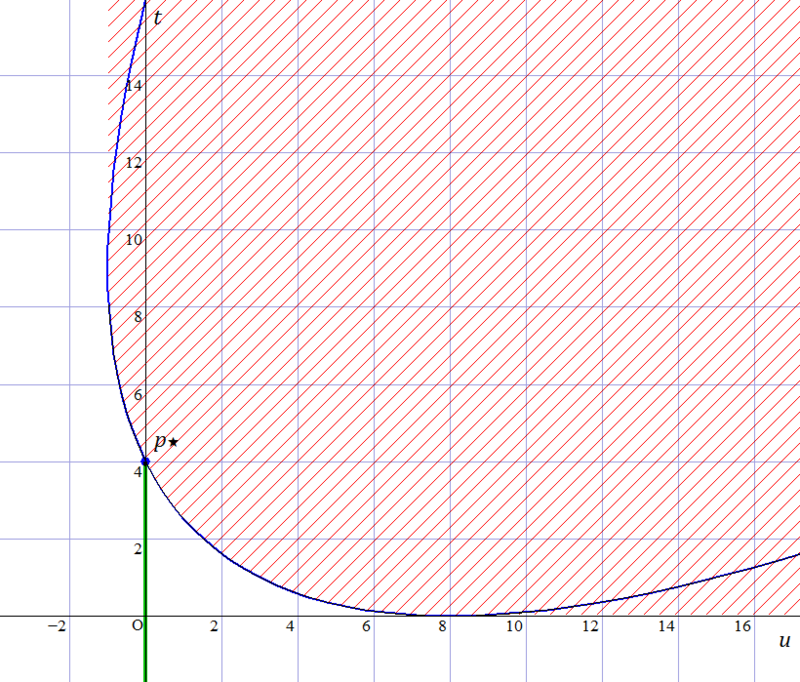
一般に主問題が凸最適化問題なら,$\mathcal{A}$ は凸領域になることが示せます.
いま,$\mathcal{B} = \{(0,0,t) \mid t < p^\star \}$ とします(上図の緑色領域).このとき$\mathcal{A}$,$\mathcal{B}$ は共有点をもたない凸領域なので,ある超平面があってこの2つを分離することが出来ます(separating hyperplane theorem).つまり,ある $(\tilde\lambda, \tilde\nu, \mu) \not= 0$ と $\alpha$ があって,
- $(u, v, t) \in \mathcal{A} \Rightarrow \tilde\lambda^\top u + \tilde\nu^\top v + \mu t \ge \alpha$
- $(u, v, t) \in \mathcal{B} \Rightarrow \tilde\lambda^\top u + \tilde\nu^\top v + \mu t \le \alpha$
ここでもしある $i$ について $\tilde\lambda_i < 0$ とすると,ある $(u,v,t) \in \mathcal{A}$ をとったとき,$u_i$ の座標をどんどん大きくすると分離平面を突き抜けることになりますが $\mathcal{A}$ の定義からそのようになっていはいけない($u_i$ の座標を大きくしても $\mathcal{A}$ に属したままでないとけない)ので矛盾します.$\mu$ についても同様のことが言えます.なので $\tilde\lambda \ge 0, \mu \ge 0$ です.
また,$\mathcal{B}$ に属する $u,v$ の座標は $0$ で,$t < p^\star$ であるので,分離平面の式から $\mu p^\star \le \alpha$ です.これらを踏まえると,任意の点 $x \in D$ について,
\[
\sum_{i=1}^m \tilde\lambda_i f_i(x) + \tilde\nu^\top(Ax-b) + \mu f_0(x) \ge \alpha \le \mu p^\star
\]
です.
ここでもし $\mu > 0$ (分離平面は $t$ 軸方向に平行ではない) と仮定すると,定式を $\mu$ で割って
\[
L(x, \tilde\lambda / \mu, \tilde\nu / \mu) \ge p^\star
\]
となり,つまり $\lambda = \tilde\lambda / \mu$, $\mu = \tilde\nu / \mu$ とおけば  となります.これはまさに強双対性を示唆するものです.
となります.これはまさに強双対性を示唆するものです.
では $\mu=0$ (分離平面が $t$ 軸に平行) の場合はどうでしょうか.詳細は疲れてきたので省きますが,Slater の条件と,$A$ が行フルランクであるという仮定を使えば,そのようなケースは存在しないということが言えます.
最適性条件
強双対性が成り立てば双対問題をかわりに考えればいいことが分かりました.しかし実際にそれを解く,つまりにはどうすればいいでしょうか.
$x^\star$, $(\lambda^\star, \nu^\star)$ がそれぞれ主問題,双対問題で最適解となるための必要条件を与えるのがKKT条件です.
相補性条件
強双対性が成り立っていると仮定した上で,$x^\star$, $(\lambda^\star, \nu^\star)$ をそれぞれ主問題,双対問題の最適解とします.このとき,


です.最後の不等式は各変数が主問題,双対問題の実行可能解であるることから $\lambda^\star \ge 0$,$f_i(x^\star) \le 0$,$h_i(x^\star)=0$ であることを用いています.これより道中の不等号は等号なので,
\[
\lambda^\star_i f_i(x^\star) = 0
\]
が成り立ちます.つまり制約関数とそれに対応するラグランジュ乗数のどちらかは必ず $0$ になります.これを相補性条件と呼びます.
勾配=0
ここで簡単のため,各関数 $$ は各点で微分可能 (したがってラグランジュ関数も微分可能) とします.
先ほどの項でも示しましたが,$x^\star$ は  の minimizer なので,$x=x^\star$ における偏微分は $0$ でなければなりません.つまり,
の minimizer なので,$x=x^\star$ における偏微分は $0$ でなければなりません.つまり,
\[
\nabla f_0(x^\star) + \sum_i \lambda^\star_i \nabla f_i(x^\star) + \sum_i \nu^\star_i \nabla h_i(x^\star) = 0
\]
でなくてはなりません.
KKT 条件は,主問題と双対問題の制約条件と,上記の相補性条件と勾配=0の条件から成り立ちます.列挙すると以下のとおりです.
- $f_i(x^\star) \le 0$
- $h_i(x^\star) = 0$
- $\lambda^\star_i \ge 0$
- $\lambda^\star_i f_i(x^\star) = 0$
- $\nabla f_0(x^\star) + \sum_i \lambda^\star_i \nabla f_i(x^\star) + \sum_i \nu^\star_i \nabla h_i(x^\star) = 0$
これまでに見たように,問題が強双対性を満たしかつ $(x^\star, \lambda^\star, \nu^\star)$ が主問題/双対問題で最適解なら,$(x^\star, \lambda^\star, \nu^\star)$ はKKT条件を満たします.つまりKKT条件は最適解であるための必要条件です.
では,逆はどうでしょうか.実は,主問題が凸の場合は,KKT条件は最適解であるための十分条件になっていることが言えます.細かい証明は省略しますが,ある $(\tilde{x}, \tilde\lambda, \tilde\nu)$ がKKT条件を満たすとすると,相補性条件のあの式みたいな感じで式変形をすれば $g(\tilde\lambda, \tilde\nu) = f_0(\tilde{x})$ が言えます.
したがって,主問題が凸でかつ各関数が微分可能な場合は,KKT条件に沿って最適解を達成する変数を求めることができます.
その他
- 今まで最小化問題を考えていましたが,代わりに最大化問題にしても同様の議論が成り立ちます.不等号制約関数で向きが逆になったりしても同様.
- Boyd本には上記で書いた解釈以外にも様々な解釈(conjugate function,min-max,ゲーム等)が載っています.
- 非凸の場合には具体的にはどうすればいいのかとかは僕が見た限り書かれていませんでした.一般には綺麗に解けないということなんでしょうか.
- 等号制約は線形のものばかり扱われましたが,線形以外だとどうでしょうか.Boyd本のExercise 5.21に例があるのですが,等号制約関数が凸であるのに強双対性が成り立たない例があります.次のようなものです:$\max_{x\in \mathbb{R},y>0} e^{-x}$ $\mbox{subject to}$ $x^2/y=0$.主問題の最適解は $1$ ですが,双対問題の最適解は $0$ になってしまいます.
- ラグランジュの未定乗数法は,等号制約しかない場合にKKT条件を使って最適解を解析的に求める手法のこと(だと思います).
まとめ
- 強双対性が成り立つと主問題の代わりに考えやすい(かもしれない)双対問題を考えれば良くなって便利.
- たとえば,主問題で変数の個数が多いが制約の個数が少ないような場合,双対問題では変数の個数が少なくなって解きやすくなる可能性がある.
- 主問題が凸(目的関数と不等号制約関数が下に凸で等号制約関数が線形)でSlaterの条件が成り立つなら強双対性が成り立つ.
- KKT条件 = 主問題の条件 + 双対問題の条件 + 相補性条件 + 勾配=0の条件
- 強双対性が成立し,かつ目的関数と各制約関数が微分可能な場合,KKT条件は各変数が最適解を取るための必要条件になっている.
- 実際に問題を解きたい場合は,まず主問題に強双対性が成り立つことを確認した上で,KKT 条件にしたがって解けば良い.
- 主問題が凸じゃない場合に強双対性が成り立つかはちょっと考える必要があるかもしれません.
- 指標の1つとして,等号制約が線形でない場合は,$\mathcal{A}$,$\mathcal{B}$ の分離平面で $t$ 軸に平行なものが存在しなければセーフ(のはず).