M.Kusumoto, and Y.Yoshida . "Testing Forest-Isomorphism in the Adjacency List Model." ICALP 2014, to appear.
修論の成果で投稿した論文が国際会議のICALP2014に採択されました.
ICALP(International Colloquium on Automata, Languages and Programming) は理論計算機科学(理論系アルゴリズム,計算量理論,言語・オートマトン,プログラミング言語理論など) を扱う国際会議です.運営はEATCSというヨーロッパの理論計算機科学の団体によって行われ,会議は毎年ヨーロッパの色々なところを転々としながら開催されるようです.今年はデンマークのコペンハーゲンで開催されます.
ICALPは理論系アルゴリズム界隈の会議の中でも上位レベルのものとして知られています.たとえば Microsoft Academic Search の引用数順で会議一覧を見てみると,上から4番目にあることが分かります.(共著者の吉田さん曰くヨーロッパ内の会議ではトップとのこと.)
論文は NII の吉田さんとの共著です.吉田さんは後述する性質検査アルゴリズム分野のプロで,今回の論文もその性質検査アルゴリズムに関するものになっています.
中身の概要
論文はざっくり言うと「木の同型性判定を,入力グラフのごく一部分だけを見て近似的に解くためのアルゴリズムの提案」がメインです.
グラフ同型性判定問題とは,2つのグラフが与えられたときに,頂点の名前を付け替えることで2つを全く同じものにすることが可能かどうかをyes/noで答える問題です.
例えば下の図のようなグラフが入力なら A→1,B→2,… という付け替えをすることで同じものにできるのでyes(同型)であると答えるのが正解,といった感じです.
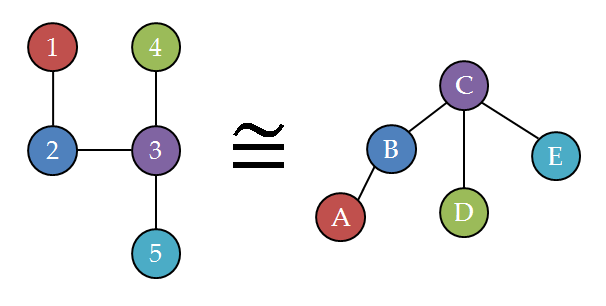
さて,冒頭で「入力のごく一部分だけを見て解く」と書いたのですが,普通に考えるとそんなことは不可能です.例えば,辺が全く無いグラフと,辺が1本だけあるグラフが同型かどうか調べたい場合,同型ではない証拠としてその1本だけある辺を探さなければならないので必然的にグラフ全体を見ることになってしまいます.
しかしここで問題をある程度緩和し,アルゴリズムが乱択になるのを許すことで,入力を一部だけ見て同型性判定問題を解けるようになります.
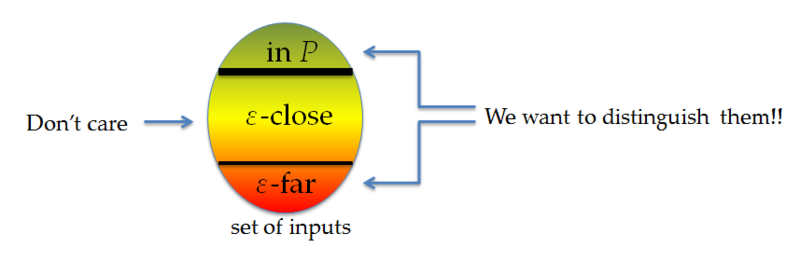
$n$ をグラフの頂点数とし,また,問題の緩和のためにパラメータ $0<\varepsilon<1$ を導入します.論文では,オリジナルのyes/no判定問題を,「2つの入力グラフが同型である」か「一方のグラフの辺を $\varepsilon n$ 本追加・削除したとしてももう一方のグラフに同型に出来ない(つまり同型から程遠い)」かの2つを区別する問題に緩和します.そのうえで,この問題がグラフの $\mathrm{polylog}(n)$ 箇所だけを見ることで任意に高い確率で解くアルゴリズムを構成しました.$\mathrm{polylog}(n)$ は $n$ が十分大きいとき,$n$ に比べてずっと小さいということに注意してください.
このような風にして問題を緩和して解く分野が性質検査と呼ばれる分野です.性質検査では,緩和した問題を解くことを「検査する」と呼んだりします.
性質検査分野への貢献
性質検査分野は1998年前後あたりから O.Goldreich や D.Ron らによって理論界隈で提唱された比較的新しい分野です.問題を緩和しているとはいえ線形時間より真に高速に解ける(爆速),理論的にも大掛かりな道具や手法が満載ということで,理論系アルゴリズムのトップ会議(STOC,FOCS,SODA)でも毎年何本か論文が採択されています.
理論屋の主な興味は,問題を緩和することによって,どのような特徴を持った問題が解けるようになるのかをある程度包括的に調べることです.つまり,さきほどの節で問題を緩和して解けるようにするみたいなことを書きましたが,緩和しさえすればどんな問題でも解けるようになるというわけではなく,依然として(入力を全部見ないと)解けないものもいっぱいあるので,それを理論的にまとまった形で分類したい,ということです.
性質検査の枠組みの中で知見が深められている分野の1つがグラフ理論です.入力が密グラフ(隣接行列)である場合は「定数時間*1で検査できる性質の必要十分条件」が知られており,疎グラフ(隣接リスト)の場合も,各頂点の次数がある定数以下であると入力に制限が付いている場合はある程度広い性質が定数時間で検査できることが知られています.
ところが疎グラフで次数の制限が無い場合がどうなのかということについては,あまりよく知られていませんでした.もともと次数制限版ばかり考えられていたのはその方が問題が解きやすくなるからという面があるのですが,次数制限されたグラフというのはグラフ全体からするとかなり限られたものになってしまっています.
問題が解きやすくなるというのは,たとえば,次数が制限されていれば頂点をランダムに選んでそこから距離が定数の部分を全部探索するといったことができますが,次数の制限が無い場合はそういったことはできません.なぜなら,探索している最中で次数がとても大きい点に突っ込んでいってしまった場合,そこにつながっている辺を全て見ると多くの部分を見る羽目になってしまうからです.
そこで,解ける範囲で入力をある程度制限しつつも,次数の制限を外した場合にどういった性質が検査できるのか? という課題に我々は焦点を当てました.入力が木であるのはだいぶ制約として強い気がしますが,それでも証明するのは全く自明ではありません.
また,論文では同型性判定を道具にして,入力として木が与えられたとき,任意の性質を $\mathrm{polylog}(n)$ 箇所だけ見ることで検査できることを証明しました.この証明には STOC'11 の Newman, Sohler が使った手法と類似のものを用いています.
ここに至るまでの過程
ここからは回想です.今回の結果はなかなか難産でした.まず修士1回生あたりのころからどういう問題に取り組めばよいかどうかをずっと模索していた気がするのですが,最初に目星を付けた問題が実はよく調べてみると既に解かれていたり,そもそも取り組むべき問題を探したところでそれが解けるのかどうかよく分からなかったりと色々遠回りをしました.今回の問題に取り組むことが決まったのは修士1回生の終わりの頃でした.
証明の方針自体は最初からなんとなく決まっていたのであとはそれを細かく解析するだけだろうと思っていたのですが,いざ始めてみると細かい部分がとても大変で,一度は投げ出し気味になってしまいました.これが修士2回生の4月~6月頃です.で,さすがに放置するのもなんなので一旦まとめて別のある会議に出したものの,しばらくしてから見返してみると証明がかなりいい加減で,会議からnotificationが返ってきたあたりから本格的に修正していきました.このとき会議から返ってきた査読のレビューがかなり的確で,ある意味無くしていたモチベーションを回復するきっかけになったような気がします.これが修士2回生の12月~1月あたりです.1月は本当に証明の修正や,論文の流れを追いやすくするために証明の概要を章の冒頭に書いたりをひたすらやっていました.
余談
アルゴリズムの厳密な計算量は $\log(n)^{2^{\mathrm{poly}(1/\varepsilon)}}$ とかになっていて実用的には超マッシブなのでそのまま実用で使うのは難しいと思われる,理論と実用のギャップはとても大きい.
*1:問題の緩和の際に導入したパラメータ$\varepsilon$は定数だと見なします