2019/06/30 に arXiv にアップロードされた論文である The Ramanujan Machine: Automatically Generated Conjectures on Fundamental Constants を読んだのでその概要をメモしようと思います。
概要
円周率 $\pi$ や自然対数の底 $e$ といった数学の定数を含む式は規則的な項を持つ連分数で表現できることが知られています。例えば wikipedia からの引用ですが以下のような等式が成り立つようです。
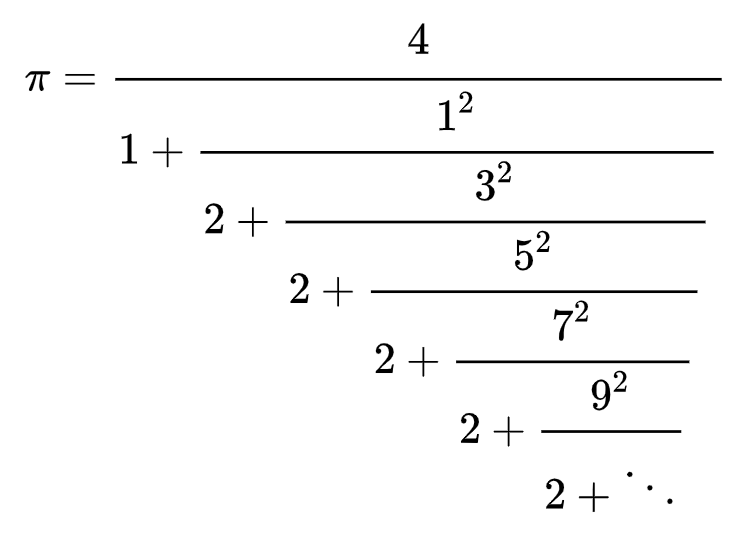
論文ではこのような形の等式に関する予想をコンピューターに自動で発見させる手法を提案しています。結果として、これまでに知られていなかった予想を複数個得られたと著者は報告しています。以下は見つかったとされる予想の一例です。
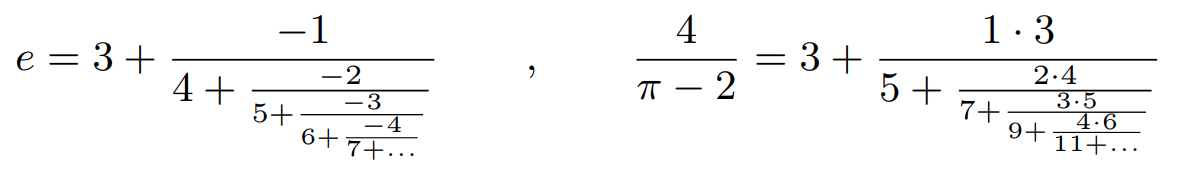
著者らの発見したこれらの等式には数学的な証明はありません ("予想"であるため) が、数値計算によって小数点以下50桁以上が一致することを確認しているようです。発見された予想は著者らのプロジェクトページにまとまっています。
論文タイトルは数学者のラマヌジャンから来ており、著者らのアプローチでは数学的な証明を一切経ずに予想を得ることから取っているのだと思います。
問題設定
$c$ を関心の対象となる定数 ($e$, $\pi$, ...) とします。求めたいのは整数係数多項式 $\alpha, \beta, \gamma, \delta$ で以下を満たすようなものです。
ここで、$\mathrm{GCF}(\alpha, \beta)$ は $a_n = \alpha(n)$ と $b_n = \beta(n)$ を一般項として持つ以下のような連分数を表すとします。

やりたいことは等式を満たす多項式の組をいろいろ見つけることです。
手法
おもしろ等式予想を見つける方法として、両側探索的な方法と勾配法をベースにした方法の2種類を提案しています。
両側探索
等式の左辺 $\gamma(c) / \delta(c)$ と右辺 $\mathrm{GCF}(\alpha, \beta)$ として考えられる候補をそれぞれ独立に列挙して、数値計算による値が一致しているものを選び出す方法です。
最初の列挙では精度の低い状態で計算して、一致していた場合はさらに精度を上げて検算することで計算効率を上げているようです。
割と普通っぽい(?)方法です。これによって $c=\zeta(3)=\sum_{n=1}^{\infty} 1 / n ^ 3$ (アペリーの定数) に対して新規の予想を得られたと報告しています。

勾配法のような何か
元の解きたい問題を最適化問題とみなします。

この問題では変数の取りうる範囲は離散領域ですが、取りうる範囲を実数に連続緩和することで勾配法のようなアプローチを取り入れようとしています。
具体的には、以下のようにしています。
- 初期値は複数個の候補を取ります。論文では1つのパラメータをあらかじめ決めた領域から等間隔に取っているようです。
- まずは勾配に沿ってそれぞれの候補を更新します。
- 次に、(恐らく候補が同じようなところに収束するのを防ぐために) 候補同士に斥力をかけて分離させることをします。
- 勾配による更新と斥力による更新を繰り返して、最終的には候補のすべてのパラメータが整数になるように調整します。損失関数を 0 にするような候補が存在すればそれはおもしろ等式ということになり、無事ハッピーな気持ちになります。
以下は論文の図の引用です。損失関数を 0 にする領域(図の水色の領域)が曲線の和集合のようになっているのが特徴的な感じがします。

その他
著者らはここからコミュニティを形成していくことに積極的なようで、プロジェクトページでは発見した予想に証明をつけてくれる人や、このプログラムを GIMPS のようなノリで動かしてさらに多くの予想を発見するのに貢献してくれる人を募集しているようです。(証明付けるのとかメッチャ大変そうなのにそんな気楽にできるもんなのか?という気はしますが…。)
連分数の収束率は多項式 $\alpha, \beta$ の次数の比によって大きく変わるようで、論文の Appendix にはその証明が記されています (僕はちゃんと読んでませんが)。
論文だと詳細がかなり端折られている (学習率や初期値のサンプル方法や、勾配とか反発の計算方法など) 箇所があるので本当に細部を知りたいなら公開されているコードを追う必要があるのだと思います。また、勾配法によって発見された等式があったのかどうかについては特に記述がないので、勾配法の良し悪しも論文だけからだとあまりよくわかりません。
有名な数学の定数で、今回の手法で試したけど等式の予想が見つからなかったものも数多くあるようです。例えばオイラーの定数 $\gamma$ などが今回そうだったようです。これらに対しても何らかの表現方法を自動で探す方法があるといいね、といった話をして論文は締めくくられています。
感想
まず問題設定の仕方がうまいと思いました。今回のような定数を含む等式の発見というタスクは伝統的なアプローチのように証明を構成することから入ろうとするとメチャクチャ大変(というか今の技術だと無理?)ですが、一方で適当に思いついた式が合ってそうかどうかはコンピューターなら一瞬で検証できるので、証明の構成を完全に回避して探索を走らせるのはなかなかコンピューター向けな気がします。
一方でこのようなことを取り組みにあたってはリスクもあったと思います。僕が想像できるのは、探索してもすでによく知られているような式しか発見できず、新しい発見に繋がらない可能性です。そのようなリスクがあった上でも実装を突き進めてちゃんと新しい発見をしたのは賞賛に値するのではないでしょうか。
とはいえ、見つかった式が本当にこれまで未知だったものなのかというのは十分に調べきれているのか(というかどこまで調べれば新しい発見だと胸を張って言えるのか?)は少し心配ではあります。が、reddit に議論スレがあって誰も新規性についての指摘などをしていないのを見るに、別に大丈夫なのかもしれません。
数学的定数に関する等式以外の分野でも未知の予想などを発見しうるアルゴリズムはもしかしたら作れるのかもしれません。誰かにやってみてほしいです。(?)